Forelesning om matematikk om emnet "tegn på vinkelrett på to plan." Perpendikulære plan, betingelsen for perpendikulæritet av plan Hvis planet er vinkelrett fra to parallelle

Denne artikkelen er viet vinkelrette plan. Definisjoner og notasjoner vil bli gitt sammen med eksempler. Tegnet på vinkelrett av fly og betingelsen som det er oppfylt under vil bli formulert. Løsninger på lignende problemer vil bli diskutert ved hjelp av eksempler.

Yandex.RTB R-A-339285-1

Hvis det er en vinkel mellom kryssende linjer, kan vi snakke om å definere vinkelrette plan.

Definisjon 1

Forutsatt at vinkelen mellom vinkelrette linjer er 90 grader, kalles de vinkelrett.

Betegnelsen på vinkelrett er vanligvis skrevet med tegnet "⊥". Hvis betingelsen sier at planene α og β er perpendikulære, har oppføringen formen α ⊥ β. Bildet nedenfor viser i detalj.

Når det er gitt i fangsten at planet α og β er vinkelrett, betyr dette at α er vinkelrett på β og omvendt. Slike plan kalles gjensidig vinkelrett. For eksempel er veggen og taket i et rom gjensidig vinkelrett, siden når de krysser hverandre danner de en rett vinkel.

Perpendikularitet av fly - tegn og tilstand for vinkelrett

I praksis kan du støte på oppgaver der det er nødvendig å bestemme vinkelrett gitte fly. Først må du bestemme vinkelen mellom dem. Hvis det er lik 90 grader, anses de vinkelrette fra definisjonen.

For å bevise vinkelrettheten til to plan, brukes tegnet på vinkelrettheten til to plan. Formuleringen inneholder begrepene en vinkelrett linje og et plan. La oss skrive presis definisjon tegn på vinkelrett i form av et teorem.

Teorem 1

Hvis ett av to gitte plan skjærer en linje vinkelrett på det andre planet, så er de gitte planene vinkelrett.

Beviset er tilgjengelig i geometrilæreboka for 10. - 11. klassetrinn, der det finnes Detaljert beskrivelse. Det følger av tegnet at hvis et plan er vinkelrett på skjæringslinjen til to gitte plan, så er det vinkelrett på hvert av disse planene.

Det er en nødvendig og tilstrekkelig betingelse for bevis. La oss vurdere dem for perpendikulæriteten til to gitte plan, som brukes som en sjekk av deres perpendikularitet, plassert i et rektangulært koordinatsystem av tredimensjonalt rom. For at beviset skal være gyldig, er det nødvendig å anvende definisjonen av normalvektoren til et plan, som bidrar til å bevise den nødvendige og tilstrekkelige betingelsen for vinkelrettheten til plan.

Teorem 2

For at vinkelrettheten til kryssende plan skal være åpenbar, er det nødvendig og tilstrekkelig at normalvektorene til de gitte planene skjærer hverandre i rette vinkler.

Bevis

La et rektangulært koordinatsystem spesifiseres i tredimensjonalt rom. Hvis vi har n 1 → = (A 1, B 1, C 1) og n 2 → = (A 2, B 2, C 2), som er normalvektorer for de gitte planene α og β, er det nødvendig og tilstrekkelig tilstand vinkelrettigheten til vektorene n 1 → og n 2 → vil ta formen

n 1 → , n 2 → = 0 ⇔ A 1 · A 2 + B 1 · B 2 + C 1 · C 2 = 0

Herfra får vi at n 1 → = (A 1, B 1, C 1) og n 2 → = (A 2, B 2, C 2) er normalvektorer av gitte plan, og for virkeligheten av perpendikulæriteten til α og β det er nødvendig og tilstrekkelig, slik at skalarproduktet av vektorene n 1 → og n 2 → er lik null, og derfor har formen n 1 → , n 2 → = 0 ⇔ A 1 · A 2 + B 1 · B2 + C1 · C2 = 0.

Likestillingen er oppfylt.

La oss se nærmere på eksempler.

Eksempel 1

Bestem perpendikulæriteten til planene spesifisert i det rektangulære koordinatsystemet O x y z til det tredimensjonale rommet spesifisert av ligningene x - 3 y - 4 = 0 og x 2 3 + y - 2 + z 4 5 = 1?

Løsning

For å finne svaret på spørsmålet om vinkelrett, må du først finne koordinatene til de normale vektorene til de gitte planene, hvoretter du kan sjekke vinkelrett.

x - 3 y - 4 = 0 er generell ligning plan, hvorfra du umiddelbart kan transformere koordinatene til normalvektoren, lik n 1 → = (1, - 3, 0).

For å bestemme koordinaten til normalvektoren til planet x 2 3 + y - 2 + z 4 5 = 1, la oss gå fra ligningen til planet i segmenter til den generelle.

Da får vi:

x 2 3 + y - 2 + z 4 5 ⇔ 3 2 x - 1 2 y + 5 4 z - 1 = 0

Da er n 2 → = 3 2, - 1 2, 5 4 koordinatene til normalvektoren til planet x 2 3 + y - 2 + z 4 5 = 1.

La oss gå videre til å beregne skalarproduktet av vektorene n 1 → = (1, - 3, 0) og n 2 → = 3 2, - 1 2, 5 4.

Vi får at n 1 → , n 2 → = 1 · 3 2 + (- 3) · - 1 2 + 0 · 5 4 = 3 .

Vi ser at den ikke er lik null, noe som betyr at de gitte vektorene ikke er vinkelrette. Det følger at planene heller ikke er vinkelrette. Vilkåret er ikke oppfylt.

Svar: planene er ikke vinkelrette.

Eksempel 2

Det rektangulære koordinatsystemet O x y z har fire punkter med koordinatene A - 15 4, - 7 8, 1, B 17 8, 5 16, 0, C 0, 0, 3 7, D - 1, 0, 0. Sjekk om planene A B C og A B D er vinkelrette.

Løsning

Først må du beregne skalarproduktet til vektorene til disse planene. Hvis det er lik null, kan vi bare i dette tilfellet vurdere at de er vinkelrette. Vi finner koordinatene til normalvektorene n 1 → og n 2 → planene A B C og A B D.

Fra de gitte koordinatene til punktene beregner vi koordinatene til vektorene A B → , A C → , A D → . Vi får det:

A B → = 47 8, 19 16, - 1, A C → = 15 4, 7 8, - 4 7, A D → = 11 4, 7 8, - 1.

Normalvektoren til planet A B C er vektorproduktet av vektorene A B → og A C →, og for A B D vektorproduktet av A B → og A D →. Herfra får vi det

n 1 → = A B → × A C → = i → j → k → 47 8 19 16 - 1 15 4 7 8 - 4 7 = 11 56 i → - 11 28 j → + 11 16 k → ⇔ n 1 → = 11 → = 11 56, - ​​11 28, 11 16 n 2 → = A B → × A D → = i → j → k → 47 8 19 16 - 1 11 4 7 8 - 1 = - 5 16 i → + 25 8 j → + 15 . k → ⇔ n 2 → = - 5 16 , 25 8 , 15 8

La oss begynne å finne skalarproduktet n 1 → = 11 56, - ​​11 28, 11 16 og n 2 → = - 5 16, 25 8, 15 8.

Vi får: n 1 → , n 2 → = 11 56 · - 5 16 + - 11 28 · 25 8 + 11 16 · 15 8 = 0 .

Hvis det er lik null, er vektorene til planene A B C og A B D vinkelrett, så er selve planene vinkelrette.

Svar: planene er vinkelrette.

Det var mulig å nærme seg løsningen annerledes og bruke likningene til planene A B C og A B D. Etter å ha funnet koordinatene til normalvektorene til disse planene, ville det være mulig å sjekke om betingelsen for perpendikularitet til normalvektorene til planene er oppfylt.

Hvis du oppdager en feil i teksten, merk den og trykk Ctrl+Enter

Definisjon. En dihedral vinkel er en figur dannet av en rett linje a og to halvplan med felles grense a, og som ikke tilhører samme plan.

Definisjon. Gradmålet for en dihedral vinkel er gradmålet for noen av dens lineære vinkler.

Definisjon. To kryssende plan kalles perpendikulære hvis vinkelen mellom dem er 90 o.

Et tegn på vinkelrett på to plan.

Egenskaper.

1. I en kuboid er alle seks flatene rektangler.
2. Alle dihedriske vinkler av en kuboid er rette vinkler
3. Firkantet diagonal av en kuboid lik summen kvadrater av dens tre dimensjoner.

Problemer og tester om emnet "Tema 7. "Dihedral vinkel. Vinkelretthet av fly."

• Dihedral vinkel. Vinkelretthet av fly
• Vinkelrettheten til en linje og et plan - Vinkelretthet av linjer og plan, grad 10

  Leksjoner: 1 oppgaver: 10 prøver: 1

• Vinkelrett og skrått. Vinkel mellom en rett linje og et plan - Vinkelretthet av linjer og plan, grad 10

  Leksjoner: 2 oppgaver: 10 prøver: 1

• Parallellisme av fly - Parallellitet av linjer og fly, grad 10

  Leksjoner: 1 oppgaver: 8 prøver: 1

• Vinkelrette linjer - Grunnleggende geometrisk informasjon 7. klasse

  Leksjoner: 1 oppgaver: 17 prøver: 1

Materialet om emnet oppsummerer og systematiserer informasjonen du kjenner fra planimetri om perpendikulariteten til rette linjer. Det er tilrådelig å kombinere studiet av teoremer om forholdet mellom parallellitet og perpendikularitet til rette linjer og plan i rommet, samt materiale på perpendikulær og skråstilt, med en systematisk repetisjon av det tilsvarende materialet fra planimetri.

Løsninger på nesten alle regneoppgaver kommer ned til anvendelsen av Pythagoras teorem og dens konsekvenser. I mange problemer rettferdiggjøres muligheten for å bruke Pythagoras teorem eller dens følgevirkninger av teoremet om tre perpendikulære eller egenskapene til parallellitet og perpendikularitet til plan.

Husk at plan kalles vinkelrett hvis vinkelen mellom dem er rett. Og denne vinkelen bestemmes slik. Ta punkt O på linje C, langs hvilken planene skjærer hverandre, og trekk rette linjer gjennom det i planene (Fig. 1.9a). Vinkelen mellom a og b er vinkelen mellom . Når denne vinkelen er rett, så sier de at planene er innbyrdes vinkelrette og skriver

Du har selvfølgelig allerede lagt merke til at når av de tre rette linjene a, b, c, er to vinkelrett på hverandre (fig. 2.28). Spesielt, . Derfor (basert på perpendiculariteten til en rett linje og et plan). Like måte,

Så, hvert av to gjensidig vinkelrette plan inneholder en vinkelrett på det andre planet. Dessuten fyller disse perpendikulærene gjensidig vinkelrette plan. (Fig. 2.29).

La oss bevise det siste utsagnet. Faktisk, hvis gjennom et punkt i planet a, tegner vi en rett linje

Deretter (ved teorem 5 om parallelliteten til perpendikulære).

Og for å indikere vinkelrettheten til plan, er en vinkelrett på planet tilstrekkelig.

Teorem 7. (test for vinkelrett på plan). Hvis et plan passerer gjennom en vinkelrett på et annet plan, er disse planene vinkelrett på hverandre.

La planet a inneholde en linje a vinkelrett på planet P (Fig. 2.28). Så skjærer rett linje a plan P ved punkt O. Punkt O ligger på linje C som de skjærer. La oss tegne en rett linje i planet P gjennom punktet O. Siden b også ligger i P-planet,

Denne funksjonen har en enkel praktisk betydning: planet til en dør hengt på en karm vinkelrett på gulvet er vinkelrett på gulvets plan i enhver posisjon av døren (fig. 2.1). Annen praktisk bruk dette skiltet: når du trenger å sjekke om en flat overflate (vegg, gjerde, etc.) er installert vertikalt, gjøres dette ved hjelp av en loddlinje - et tau med en last. Loddlinjen er alltid rettet vertikalt, og veggen står vertikalt hvis loddlinjen, plassert langs den, på noe tidspunkt ikke avviker.

Når du løser problemer som involverer vinkelrette plan, brukes ofte følgende tre setninger.

Proposisjon 1. En linje som ligger i ett av to innbyrdes vinkelrette plan og vinkelrett på deres felles linje er vinkelrett på det andre planet.

La planene være innbyrdes perpendikulære og skjære langs rett linje C. La videre rett linje a ligge i planet a og (Fig. 2.28). Linje a skjærer linje C i et punkt O. La oss trekke en linje b gjennom punkt O i planet P, vinkelrett på linje c. Så sånn er det. Siden , da (ved teorem 2).

Den andre setningen er det motsatte av den første.

Proposisjon 2. Linje som har felles poeng med ett av to innbyrdes vinkelrette plan og vinkelrett på det andre planet, ligger i det første av dem.

La planene være innbyrdes perpendikulære, og la rett linje a ha et felles punkt A med plan a (Fig. 2.30). Gjennom punkt A i plan a tegner vi en rett linje vinkelrett på rett linje C - skjæringslinjen mellom planene. I følge forslaget, siden det i rommet bare går en linje vinkelrett på et gitt plan gjennom hvert punkt, så faller linjene a og sammen. Siden a ligger i flyet, så ligger a i flyet

Proposisjon 3. Hvis to plan vinkelrett på et tredje plan skjærer hverandre, er skjæringslinjen deres vinkelrett på det tredje planet.

La to plan som krysser en rett linje a være vinkelrett på planet y (fig. 2.31). Deretter trekker vi gjennom et hvilket som helst punkt på linje a en linje vinkelrett på planet y. I følge Proposisjon 2 ligger denne linjen både i planet a og i planet P, det vil si at den faller sammen med linjen a. Så,

Vinkelretthet av fly Definisjon. To plan kalles perpendikulære hvis den lineære vinkelen ved kanten av den dihedrale vinkelen mellom disse planene er en rett linje.
Skilt vinkelrett på plan. Hvis et plan går gjennom en linje vinkelrett på et annet plan, er disse planene vinkelrette.
Bevis. La en Og ? - to kryssende plan, Med- linjen til deres skjæringspunkt og EN- rett vinkelrett på planet? og ligger i et flyen. A - skjæringspunkt for linjeren Og Med. I et fly? fra punkt Og vi vil gjenopprette vinkelrett, og la det være en rett linje b. Rett EN vinkelrett fly? , som betyr at den er vinkelrett på en hvilken som helst rett linje i dette planet, det vil si rette linjer b Og Medvinkelrett . Vinkel mellom rette linjer EN Og b - lineære plan en Og ? og det er lik 90°, altså Hvordan rett EN vinkelrett på en rett linjeb(bevist). Etter definisjonen av et flyen Og ? vinkelrett.

Teorem 1. Hvis vi tegner fra et punkt som tilhører en av to vinkelrette plan vinkelrett på et annet plan, så ligger denne perpendikulæren helt i det første planet.
Bevis. La en Og ? - vinkelrette plan og Med - den rette linjen i skjæringspunktet deres, A - punkt en ligger flatt Med. og ikke direkte tilhører en La vinkelrett på planet? trukket fra punkt A ligger ikke i planet , da er punktet C basen denne perpendikularen ligger i Med. fly? og tilhører ikke linjen Fra punkt A senker vi perpendikulæren AB Med. direkteLinje AB er vinkelrettplan (jeg bruker teorem 2).Gjennom rett linje AB og punkt C Skal vi tegne et fly? (en rett linje og et punkt definerer et plan, og bare ett). Det ser vi i ? flyet fra ett punkt A til rett linje BC tegnes to perpendikulære, noe som ikke kan skje, som betyr rett linje AC en.

faller sammen med rett linje AB, og rett linje AB ligger på sin side helt i planet. Teorem 2Hvis vi i ett av to vinkelrette plan tegner en vinkelrett på linjen deres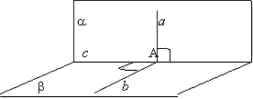
Bevis. La en skjæringspunktet, så vil denne perpendikulæren være vinkelrett på det andre planet. - vinkelrette plan og Og ? - to vinkelrette plan, linjen i deres skjæringspunkt og A - Med og ligger i et flyenrett EN Og Med. vinkelrett på en rett linje. A - skjæringspunkt for linjer I fly? fra punkt A gjenoppretter vi perpendikulæren, og lar den være en rett linje EN Ogb b. Vinkel mellom rette linjer- lineær en vinkel ved kanten av dihedral vinkel mellom flyen Og ? og det er lik 90°, siden planet EN Og ?bvinkelrett. Rett Med vinkelrett på en rett linje(ifølge bevist) og direkte EN etter tilstand.